阅读:0
听报道
文 | 张明 魏伟 陈骁
注:平安宏观团队将会陆续发布中国宏观经济研究框架系列研究,这是系列的第一篇。
平安观点
本文梳理了通货膨胀分析与预测的框架。关于CPI的分析框架主要包括三个维度:一是基于猪周期、进口价格和M1三个影响因素建立协整模型;二是基于CPI环比周期性的“环比均值法”;三是依靠产出缺口对CPI的趋势进行预测。我们将根据前两个维度得出CPI的预测值,寻找合适的权重进行加权,然后根据第三个维度对CPI预测值进行调整。
CPI的三因素协整模型:选取猪肉价格、进口价格与M1三个因素对CPI进行分析。①猪肉价格在CPI中所占权重相对较高,波动幅度较大,并且具有明显的周期性特征,能够显著影响CPI的走势。②进口价格表征“输入型通胀”的影响,中国进口商品结构中大宗原材料占比较高,进口成本价格将直接影响工业生产的整体成本,进而传导至PPI,再由PPI向下游的CPI传导。③传统的费雪方程表明货币数量对通胀起决定性作用, M1与CPI之间在经过一段时滞后呈现明显的正相关关系。利用上述三个因素建立协整模型,能够对CPI同比走势进行预测,历史数据检验显示模型拟合程度较好。
CPI预测的环比均值法:CPI中占权重较高的食品价格受到春节因素、天气变化、养殖规律等季节性因素的影响,呈现出明显的波动规律,这样的季节性规律在年内表现得相对稳定。并且,由于食品价格的波动幅度大大高于非食品价格,且所占权重并不低,食品价格的环比波动基本决定了CPI环比的走势。基于CPI环比存在的周期性特征,我们可以使用最近5年的环比均值来估算每月CPI的环比,在较大概率上不会出现趋势性偏差;然后根据CPI环比与同比数据之间的关系,计算出CPI同比的趋势。
两种模型的对比与结合:使用2015-2016年的两年数据来对上述两种CPI预测模型进行短期预测的检验,根据“误差最小化”的原则用试错法确定两者最终的权重:VAR模型最适合的权重为0.51,环比均值法的权重为0.49。对上述两种模型得出的CPI预测值进行加权平均,最终得出2017年CPI同比为1.4%。
根据产出缺口对CPI预测的修正:产出缺口与物价水平上涨率呈同向变动关系,即当产出缺口为正时,需求大于供给,形成通货膨胀压力;当产出缺口为负时,需求小于供给,形成通货紧缩压力。不过,由于产出缺口衡量的是整体价格水平,其所代表的物价上行压力很可能同时包括了CPI与PPI的走势特征。历史数据也印证了这一点,产出缺口与PPI的相关性更高。因此,尽管从当前产出缺口的走势来看,未来一段时期通胀将面临一定的上行压力,但这大部分已经反映在了近期PPI大幅上行的走势上。考虑到PPI向CPI传导的效应仍然可能造成一定影响,我们将2017年CPI预测值小幅上修0.2个百分点至1.6%。
通货膨胀作为衡量一般物价水平的指标,在宏观经济分析中的重要性不言而喻。广义的通货膨胀指标有多种,包括消费者物价指数(CPI),工业品出厂价格指数(PPI),GDP平减指数等。不过,市场分析一般所指的狭义通胀水平仍是CPI同比增速,原因在于CPI与居民生活相关程度最高。大部分国家央行在制定货币政策时,重点参考的通胀指标也是CPI。因此,本文将重点以CPI同比数据为主,构建中国通货膨胀的预测框架。
我们关于CPI的分析框架主要包括三个维度:一是基于猪周期、进口价格和M1三个影响因素建立协整模型;二是基于CPI环比周期性的“环比均值法”;三是依靠产出缺口对CPI的趋势进行预测。根据前两个维度得出CPI的预测值,寻找合适的权重进行加权,然后根据第三个维度对CPI预测值进行调整。
一、 CPI的三因素协整模型
CPI通常分为食品价格与非食品价格两大类,在食品价格当中我们选取了猪肉价格作为CPI的第一个影响因素;在非食品价格当中我们选择了进口价格指数作为CPI的第二个影响因素;而根据传统的货币数量论,对于货币供应量对于通货膨胀也将造成直接影响,因此我们选取M1作为第三个影响因素。
1.1猪肉价格与通胀
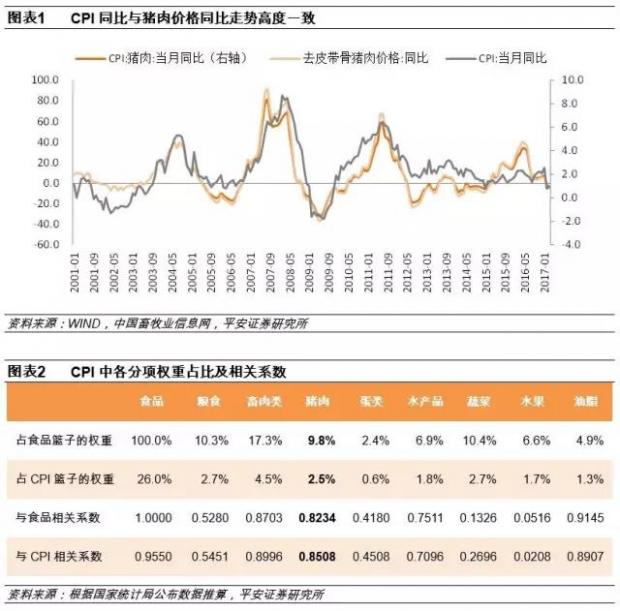
猪肉价格在相当长的一段历史时期内被宏观研究者视为分析通胀最为准确的、甚至是唯一重要的指标,因为从中国已有的2001年至2013年的猪肉价格和CPI数据来看,两者波动的周期高度一致,只是猪肉价格波幅远大于CPI的波幅。只要能准确判断猪周期波动,就基本能够判断CPI的走势。猪肉价格与CPI的相关性逻辑在于:猪肉价格在CPI中所占权重相对较高,波动幅度较大,并且具有明显的周期性特征,因此能够显著影响CPI的走势。
1)根据国家统计局最2016年1月对CPI分项进行调整后的权重,食品价格在CPI中的权重约为26%左右;而猪肉价格占食品价格权重接近10%,占CPI权重约为2.5%左右。在CPI各分项中,CPI与食品价格相关性最高,食品价格与猪肉价格相关性最高。从2005年至今的历史数据来看,CPI同比与CPI食品价格同比的相关系数高达0.95(与非食品相关系数仅为0.66),而CPI食品价格同比与CPI猪肉价格同比分项的相关系数则高达0.85。
2)由于我国生猪散养的特征,猪肉价格受到生猪养殖户活动的影响,呈现出较为明显的周期性特征:当猪肉价格上涨时,养殖户增加生猪养殖量,逐渐导致生猪供给增加,抑制猪肉价格上涨;供给持续大幅扩张以至于供过于求,猪肉价格进入下行区间,此时养殖户逐渐减少生猪养殖量,生猪供给逐渐减少,以至于供不应求,猪肉价格则重新进入上行通道。而从历史数据看,一个完整的猪周期(猪肉价格上涨到下跌的过程)一般延续3年左右的时间。
因此,猪肉价格是CPI当中波动幅度最大,且周期性最为明显的分项,这有利于我们通过猪周期的波动对CPI进行预测。值得一提的是,蔬菜价格的波动幅度也非常大,但其主要受到天气因素的影响而呈现年内规律的周期性波动,对CPI走势的影响并不明显,两者相关系数也较低。
1.2进口成本与通胀
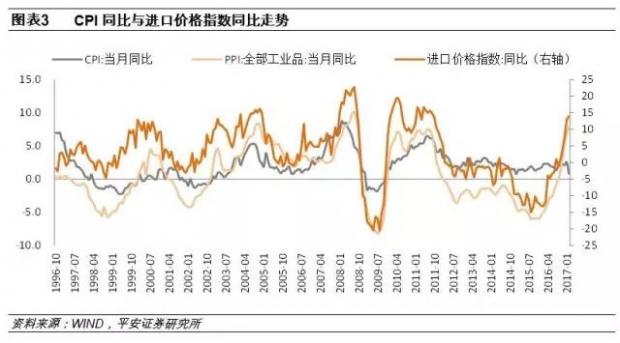
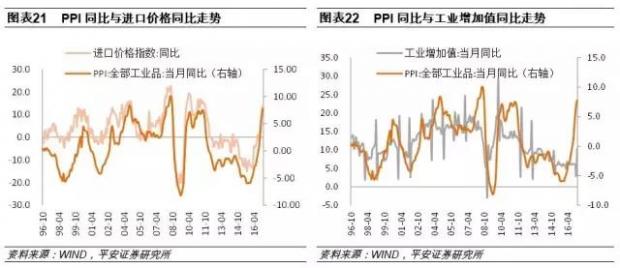
进口成本价格主要表征了“输入型通胀”的影响以及PPI对CPI的传导效应。进口成本与通胀之间的相关逻辑在于:中国进口商品结构中大宗原材料占比较高,进口成本价格将直接影响工业生产的整体成本,进而传导至工业品出厂价格(PPI),再由PPI向下游的CPI传导。
从历史数据上看,进口成本价格指数的同比增速与PPI一致性较高,同时也呈现出PPI向CPI传导的规律。总体而言进口成本价格与CPI呈现一定的错峰关系,即进口成本对CPI的传导存在一定的时滞。
1.3 M1与通胀
传统的费雪方程MV=PT衡量了货币供应量与价格之间的关系,其中M为流通中的货币数量,V为货币流通速度,P为物价水平(通胀),T为各类商品的交易总量。由此,通货膨胀水平由M、T、V三个经济变量决定。其中,货币流通速度V是由多种复杂因素决定,但变化相对缓慢;T与产出水平保持一定比例,短期内也大体稳定;因此短期来看货币数量M对于通胀P起决定性作用。
按照费雪方程的含义,流通中的货币数量最为合适的衡量指标是M1。从1995年以来的历史数据来看,M1同比增速与CPI同比增速走势之间在经过一段时滞后呈现出较为明显的正相关关系。
1.4 三因素协整模型的建模与分析
如上所述,猪肉价格同比增速、进口价格同比增速、M1同比增速三者均与CPI之间存在较为显著的相关关系,其中猪肉价格与CPI走势基本同步,进口价格和M1则与CPI走势存在一定的时滞。因此,我们利用这三个因素的时间序列建立协整模型,来拟合与估计CPI同比的走势。我们将模型的建立过程简要介绍如下:
1、指标选择
时间区间:2002年6月-2017年2月(考虑有进口成本的影响,因此取中国加入WTO之后的时间区间,可能更准确反映CPI受到进口成本的影响)
因变量:CPI同比(CPI)
自变量:M1同比(M1),猪肉价格同比(PIG),进口价格指数同比(IPT)
2、平稳性检验
对四个时间序列进行单位根检验,其结论是,进口价格同比和猪肉价格同比平稳;CPI同比和M1同比不平稳,且均为一阶单整。但是,我们将三因素与CPI同比建立VAR模型进行模型的整体检验,发现所有的单位根都落在单位圆内,这说明模型整体平稳,可以进行进一步的检验。
3、Johansen协整检验与格兰杰因果检验
将四个时间序列进行Johansen协整检验,结论是至少存在4个协整关系。在此基础上,根据AIC与SC准则得出的最小滞后阶数(2阶)进行格兰杰因果检验,证明了CPI与三个因素均存在相关关系。
4、VAR模型的建立及分析
CPI,M1,IPT,PIG四个变量建立VAR(2)模型,使用Eviews软件对模型进行估计,所得出的估计结果中,CPI序列的R2值为的0.943,表明三因素模型对于CPI的拟合程度较高(具体结果见附录1)。同时,我们对此协整模型进行样本内的动态预测,得出的预测值与CPI同比本身的相关性较高,显示模型的预测效果也较好。
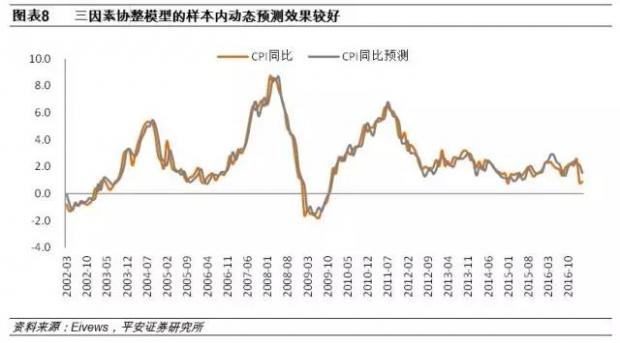
此外,我们对模型进行了脉冲响应和方差分解,得出的结果如下图所示。
脉冲响应的结果显示:进口价格对CPI的影响是先正后负,前期正向的影响上升,此后逐渐下滑并至负区间。M1对CPI是正向且持久的影响;但在前期存在波动,3期之后影响平稳递增。猪肉价格对CPI是正向且持久的影响,且前期的影响较为陡峭,3期之后影响变得逐渐平稳。
方差分解的结果显示:CPI受其序列自身的影响最大,其余三个因素影响较小;而三个因素当中,猪肉价格与M1的影响相对显著,进口价格的影响较小。

二、 CPI预测的环比均值法
除了上文所述的协整模型之外,另一个能够大致估算CPI走势的方法是环比历史均值法。
2.1 CPI环比的周期特征
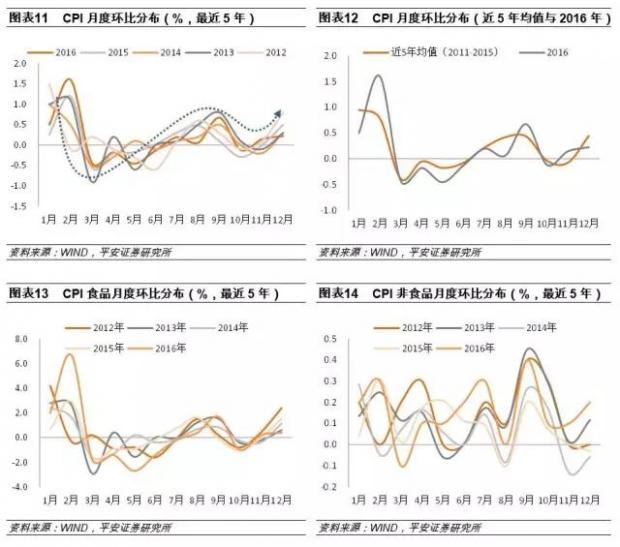
CPI月度环比数据的年内分布呈现出明显的周期性特征。从最近5年的CPI月度环比分布来看,大致呈现这样的规律:1-2月为CPI环比的相对高点;3-5月显著回落至负区间,并在低位徘徊;6-9月逐步回升,在9月达到阶段性高点后,10-11月缓慢回落,12月再度反弹。
出现这种规律的原因在于,CPI中占权重较高的食品价格受到春节因素、天气变化、养殖规律等季节性因素的影响,呈现出明显的波动规律:例如,每年1-2月由于春节因素导致的需求上升与气温下降带来的供给短缺,蔬菜、猪肉等价格一般都将出现较大幅度的上涨;而3-5月由于天气转暖带来的农产品供给回升,食品价格又将出现回落。这样的季节性规律在年内表现得相对稳定,并且由于食品价格的波动幅度大大高于非食品价格,且所占权重并不低,食品价格的环比波动基本决定了CPI环比的走势。
2.2 环比均值法的CPI预测
基于CPI环比存在的周期性特征,我们可以使用最近5年的环比均值来估算每月CPI的环比,而在较大概率上不会出现趋势性的偏差;然后根据CPI环比与同比数据之间的关系,计算出CPI同比的趋势。不过,这种预测方法的缺陷在于,只考虑了基于历史经验的季节性因素对于CPI的影响,而并未将可能发生的额外冲击计算在内。
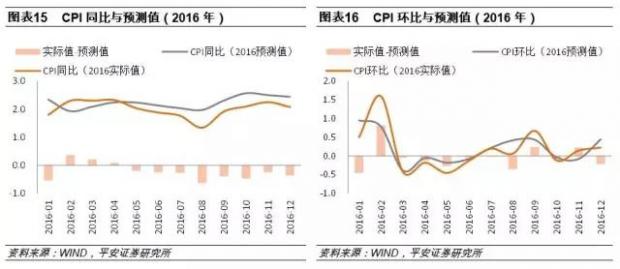
以2016年为例,我们通过环比历史均值的方法,以2011-2015年各月的CPI环比均值,作为2016年各月CPI环比的预测值;然后根据CPI环比与同比数据之间的关系,可以计算出2016年CPI同比。对比CPI实际值与预测值的月度分布可见两者趋势上大体一致,而从年度数据来看,2016年CPI同比预测值为2.2%,实际值2.0%,年度数据误差也较小。
三、 两种模型的对比与结合
3.1用历史数据验证两种模型的准确性
我们使用2015-2016年的两年数据来对上述两种CPI模型进行CPI短期预测的检验。具体步骤如下:
①VAR模型直接使用样本内预测方法,进行2015和2016年的静态预测;
②环比均值法分别使用2010-2014年CPI环比均值预测2015年CPI环比分布,使用2011-2015年CPI环比均值预测2016年CPI环比分布,再根据CPI同环比的关系计算得出CPI同比走势。
③对VAR模型的预测值和环比均值法预测值赋予不同的权重,根据“误差最小化”的原则用试错法确定两者最终的权重。结论为:VAR模型最适合的权重为0.51,环比均值法的权重为0.49。
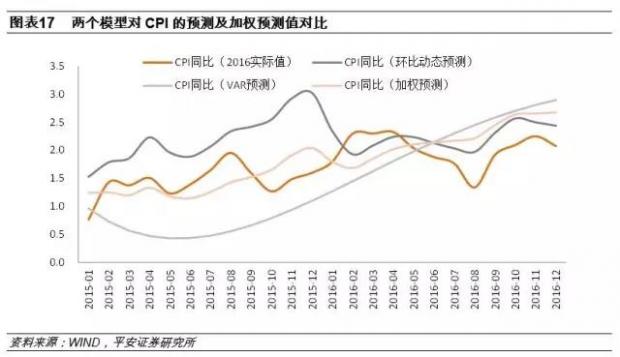
如下图所示,两种方法得出的CPI预测值之间能够相互修正(如2015年四季度),两者加权之后能够得出一个拟合度相对较高的预测值。从年度数据看,2015与2016年CPI同比加权预测值为1.4%和2.2%;CPI同比实际值分别为1.4%和2.0%,模型预测的准确度较高。
3.2 2017年CPI同比的加权预测
按照上述两种模型的加权平均对2017年的CPI数据进行预测,所得预测结果及趋势如下:
①用VAR模型进行样本外预测,得出2017年CPI同比为1.7%;
②用环比均值法进行2017年CPI环比预测,进而推算CPI同比;得出2017年CPI同比为1.1%;
③按照VAR预测值0.51,环比均值法预测值0.49的权重,计算两种预测值的加权平均值;最终得出2017年CPI同比为1.4%。
四、 产出缺口对CPI预测的修正
4.1产出缺口与CPI的理论基础
产出缺口是实际产出与潜在产出的差值,主要反映经济资源利用的程度。根据新凯恩斯主义相关理论,潜在产出是一国在现有的劳动力、资本、技术充分利用下所能达到的生产水平;根据菲利普斯曲线,实际产出对潜在产出的偏离与物价水平上涨率呈同向变动关系,即当产出缺口为正时,需求大于供给,形成通货膨胀压力;反之当产出缺口为负时,需求小于供给,形成通货紧缩压力。众多实证研究也发现产出缺口与CPI存在较强的相关关系,通过产出缺口可以间接预测CPI的走势。
不过值得一提的是,产出缺口之所以能够预测通胀,是因为在许多产品领域存在普遍的价格粘性。如果不存在价格粘性,市场即时出清,产出缺口对通货膨胀也就失去了预测能力。中国的CPI变动主要由食品价格的波动驱动,由于食品领域并不存在广泛的价格粘性,利用产出缺口预测中国的CPI变动缺乏严谨的理论基础,仅适合作为调整和补充。
4.2 产出缺口与CPI同比的关系
为描述产出缺口,我们采用1999年至2017年第一季度的GDP环比数据进行计算。首先对GDP环比数据做季节性调整,再通过HP滤波法分解出趋势项和周期项,其中趋势项描述潜在产出的变动,周期项描述产出缺口的变动。
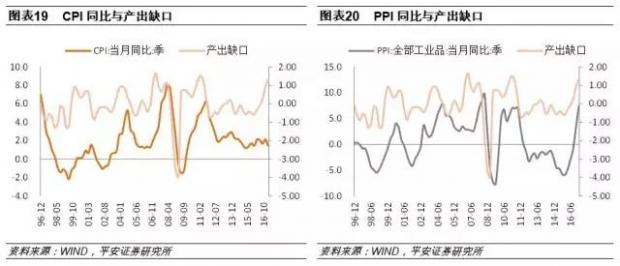
对比产出缺口与CPI同比的走势,我们发现两者显示出较强的相关性,并且产出缺口的变动大致领先于CPI的变动1~2个季度。但同时,由于产出缺口衡量的是经济整体的价格水平,我们进一步考察产出缺口与PPI之间的关系,发现在数据拐点处的相关性较CPI更高。因此,产出缺口所代表的物价上行压力,很可能同时包括了CPI与PPI两者的走势特征。
我们观察到近期的数据显示,从2016年起产出缺口不断攀升并由负转正,目前正处于高位,这实际上与PPI同比的大幅攀升相一致;而CPI同比走势仍然较为温和,一定程度上显示了PPI向CPI传导渠道的阻滞。
从产出缺口的走势来看,未来一段时期通胀将面临一定的上行压力,但这大部分已经反映在了近期PPI大幅上行的走势上。考虑到PPI向CPI传导的效应仍然可能造成一定影响,我们将2017年CPI预测值小幅上修0.2个百分点至1.6%。
附录1:PPI的影响因素
工业品出厂价格(PPI)也是市场关注度较高的物价指标之一,并且PPI向CPI存在一定程度的传导效应。我们简单构建PPI同比增速、工业品产值同比增速(需求方)与单位进口成本指数(供给方)的非限制性VAR模型,对模型进行脉冲响应分析与方差分解,比较需求方与供给方对PPI同比增速方差各自的贡献。
1、指标选择
时间区间:1996年10月-2017年2月
因变量:PPI同比(PPI)
自变量:工业增加值同比(IAV),进口成本价格同比(IPT)
2、平稳性检验
对四个时间序列进行单位根检验,其结论是,进口价格同比(IPT)和PPI同比(PPI)平稳;工业增加值同比(IAV)不平稳。但是,我们将三因素与CPI同比建立非限制性VAR模型进行整体检验,发现所有的单位根都落在单位圆内,说明模型整体平稳,可以进行进一步的检验。
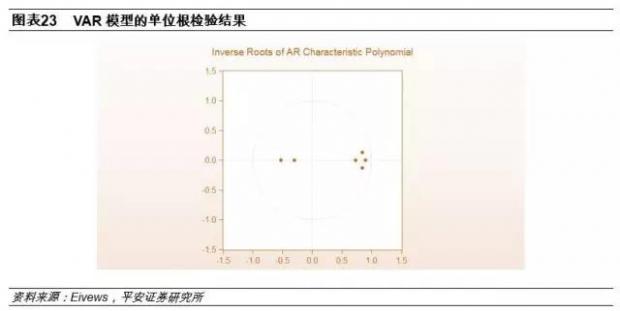
3、Johansen协整检验与格兰杰因果检验
将三个时间序列进行Johansen协整检验,结论是至少存在3个协整关系。在此基础上,根据AIC与SC准则得出的最小滞后阶数(2阶)进行格兰杰因果检验,证明了PPI与两个因素均存在相关关系。
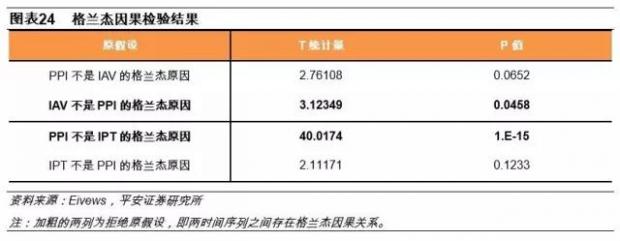
4、VAR模型的建立及分析
PPI,IAV,IPT三个变量建立VAR(2)模型,使用Eviews软件对模型进行估计,所得出的估计结果中,PPI序列的R2值为的0.977(具体结果见附录3),表明两个因素对于PPI的拟合程度较高。
我们对此协整模型进行样本内的动态预测,得出的预测值与PPI同比本身的走势高度一致,显示模型的短期预测效果较好;同时,我们对此模型进行样本外的预测(预测区间分别取2015年至今,以及2016年至今),得出结果显示VAR模型的预测值能够一定程度上表征PPI的大体趋势。
此外,我们对模型进行了脉冲响应和方差分解,得出的结果如下图所示。
脉冲响应的结果显示:进口价格对PPI的影响是先正后负,前期正向的影响上升,此后逐渐下滑并接近零;工业增加值对PPI的影响正向而持久,其影响在2-6期逐渐增强,7期以后变得较为平缓。可见,供给端和需求端在短期都对PPI有正向的影响;但供给端的影响短暂且逐渐递减,而需求端的影响则更为持久,且呈现递增后逐步稳定的态势。
方差分解的结果显示:PPI受其序列自身的影响最大,在10期之后贡献率仍超过80%,而其余两个因素对PPI的贡献相对较小。其中,工业增加值所代表的需求端对PPI的贡献率呈递增态势,在10期后升至15%左右;但进口价格所代表的供给端对PPI的贡献率影响则一直偏小。
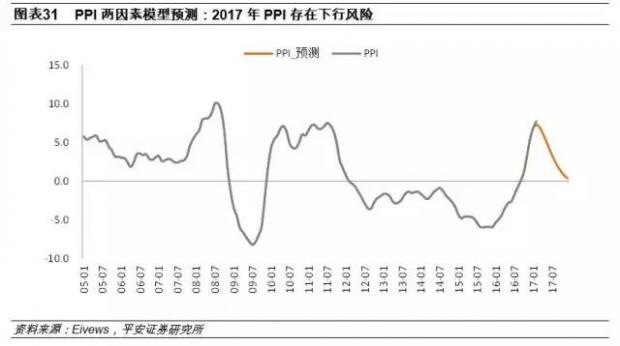
5、对2017年PPI走势的预测
最后,我们使用上述建立的两因素VAR模型对2017年的PPI走势进行样本外预测。从趋势上看,PPI同比在2017年存在下行的风险。
话题:
0
推荐
财新博客版权声明:财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有,未经博主及/或相关权利人单独授权,任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点,不代表财新网的立场和观点。




 京公网安备 11010502034662号
京公网安备 11010502034662号 